Dans les années 70, des mathématicien et des informaticiens ont inventé des méthodes de calcul, complexes pour les humains, mais relativement simples (nous y reviendrons) pour les ordinateurs et autres automates. Ce que nous appellerons le « hash » (fonction de hachage) peut se résumer de manière très simple.
Introduction

- On rentre un élément de très grande taille (une image, un programme informatique, le contenu de votre ticket de votre caisse enregistreuse, …) et on obtient en sortie une « empreinte », par exemple un texte court de 512 caractères (pour un ordinateur, c’est court…).
- Si on fournit exactement le même élément en entrée, on obtient à chaque fois exactement le même résultat. Ouf !
- Si on change un seul détail de la donnée en entrée, la sortie est complètement différente.
- Une empreinte de 512 caractères (techniquement dits « hexadécimaux ») laisse des milliards de milliards de possibilités différentes : un 1 suivi de 2500 chiffres, soit plusieurs de milliards fois plus que le nombre d’étoiles dans l’univers ou le nombre de grains de sable sur la Terre.
- Donc, en liant les deux points précédents, il est presque improbable au cours de votre vie que le hash de 2 entrées différentes produisent le même résultat.
- Et surtout: C’est un travail en sens unique : pour un résultat de hash donné, impossible de retrouver tout seul quelle était l’entrée. C’est simple pour un ordinateur dans un sens, il faudrait des millions d’ordinateurs testent en continue toutes les possibilités pendant plusieurs dizaines d’années pour décoder un et un seul hash !
Des exemples ? Au détour d’un document technique ou légal, vous pouvez avoir entendu parler de MD5, SHA1, SHA2, …
A quoi ça sert techniquement ?
Ça permet de vérifier que quelque chose n’a pas été modifié:
- Si on change un tout petit détail au ticket de caisse, refaire son hash donnera un résultat complètement différent et on saura que le ticket de caisse a été modifié
- Si on a n’a rien changé, refaire le hash donnera le même résultat et on saura qu’on a toujours le bon hash et que le contenu du ticket n’a pas été modifié
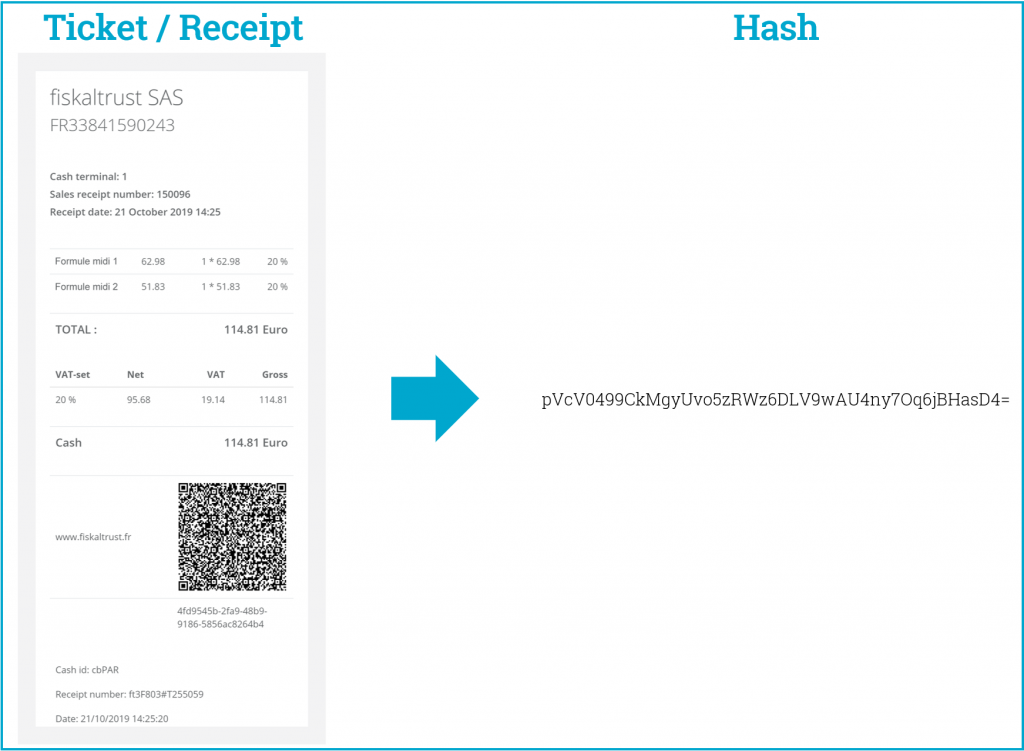
A quoi ça sert en pratique ?
Ça sert au compresseur de fichiers tels que zip: Avec le zip, il y a le hash du contenu original. On décompresse, on recalcule le hash. Si c’est différent, il y a un problème… Lequel, on ne sait pas, mais c’est déjà bien de savoir qu’il y a un problème.
Ça sert à la communication entre ordinateurs: un ordinateur n’envoie jamais une information sans envoyer un élément en plus (ca peut être un hash, mais ça peut aussi être beaucoup plus simple). L’ordinateur qui reçoit la communication et l’élément en plus refait le calcul: si c’est différent, il redemande automatiquement d’envoyer de nouveau la même communication.
Ça sert aussi à la blockchain, au login avec mot de passe, à l’inaltérabilité des justificatifs fiscaux au sein de la loi française « anti-fraude à la TVA », à la signature électronique, au stockage de données à court ou à long terme, etc..
Ça sert à quelque chose que nous appelons le chaînage et sur lequel nous reviendrons dans un prochain article…